Teorema de Bayes

A probabilidade rege nossas vidas: nós a usamos todos os dias sem ter consciência disso. Por isso, hoje falaremos sobre um dos seus teoremas mais importantes: o teorema de Bayes.

Escrito e verificado por a psicóloga Paula Villasante.

Última atualização: 27 janeiro, 2023

O teorema de Bayes é um dos pilares da probabilidade. Trata-se de uma teoria apresentada por Thomas Bayes (1702-1761) no século XVIII. Mas o que exatamente este cientista estava tentando explicar? De acordo com a Real Academia Espanhola, a probabilidade expressa, em um processo aleatório, a relação entre o número de casos favoráveis ​​e o número de casos possíveis.

Foram desenvolvidas muitas teorias sobre a probabilidade, que nos governam até hoje.. Quando vamos ao médico, ele nos receita aquilo que é mais provável que resolva o nosso problema, os publicitários dedicam suas campanhas para as pessoas que estão mais propensas a comprar o produto que pretende promover, nós escolhemos a rota pela qual provavelmente iremos demorar menos.

Uma das mais famosas leis da probabilidade é a lei da probabilidade total. Para começar, temos que considerar o que é a lei da probabilidade total. Para entendê-la, vamos dar um exemplo.

Vamos supor que, em um país aleatório, 39% da população é de mulheres. Sabemos também que 22% das mulheres e 14% dos homens estão desempregados. Então, qual é a probabilidade (P) de que uma pessoa selecionada aleatoriamente da população ativa nesse país esteja desempregada?

De acordo com a teoria da probabilidade, os dados seriam expressos da seguinte forma:

• A probabilidade de que a pessoa fosse mulher: P (M)
• A probabilidade de que a pessoa fosse homem: P (H)

Sabendo-se que 39% da população são mulheres, então deduzimos que: P (M) = 0,39.

Logo, entendemos que: P (H) = 1-0,39 = 0,61. O problema apresentado também nos dá as probabilidades condicionais:

• A probabilidade de que uma pessoa esteja desempregada, sabendo que é uma mulher -> P (P | M) = 0,22
• A probabilidade de que uma pessoa esteja desempregada, sabendo que é um homem -> P (P | H) = 0,14

Desta forma, usando a lei da probabilidade total, teremos:

P (P) = P (H) P (P | H) + P (H) P (P | H)

P (P) = 0,22 × 0,39 + 0,14 × 0,61

P (P) = 0,17

Assim, a probabilidade de que uma pessoa escolhida aleatoriamente esteja desempregada é de 0,17. Observamos que o resultado está entre as duas probabilidades condicionais (0,22 <0,17 <0,14). Além disso, está também mais perto dos homens, porque a população deste país inventado é majoritariamente masculina.

Teorema de Bayes

Agora suponhamos que uma pessoa adulta seja escolhida aleatoriamente para preencher um formulário e se observa que ela não tem trabalho. Neste caso, e considerando o exemplo anterior, qual é a probabilidade de que esta pessoa escolhida aleatoriamente seja uma mulher -P (M | P) -?

Para resolver este problema, vamos aplicar o teorema de Bayes. Assim, este teorema é usado para calcular a probabilidade de um evento tendo de antemão informações sobre esse evento. Podemos calcular a probabilidade de um evento A, sabendo também que o evento A atende determinada característica (B), que determina a sua probabilidade.

Neste caso, estamos falando da probabilidade de que a pessoa escolhida aleatoriamente para preencher um formulário seja mulher. Além disso, esta probabilidade não será independente de que a pessoa selecionada esteja desempregada ou não.

A fórmula do teorema de Bayes

Como qualquer outro teorema, para calcular a probabilidade, precisamos de uma fórmula. Neste tipo de eventos, a fórmula é definida como:

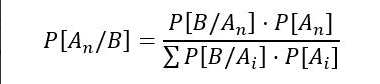
Parece complicado, mas tudo tem uma explicação. Vamos em partes. O que cada letra significa?

• Para começar, B é o evento sobre o qual temos informações prévias.
• A letra A (n) refere-se aos diferentes eventos condicionados.
• Na parte do numerador, temos a probabilidade condicionada. Esta se refere à probabilidade de que alguma coisa (evento A) ocorra, sabendo que também ocorre outro evento (B). É definida como P (A | B) e expressa como: a probabilidade de A dado B.
• No denominador, temos o equivalente de P (B). Veja a seção anterior.

Um exemplo:

Então, de volta ao exemplo anterior, suponhamos que se escolha um adulto aleatoriamente para preencher um questionário e se observa que não tem trabalho (está desempregado). Qual será a probabilidade de que essa pessoa escolhida seja uma mulher?

Bem, considerando o exemplo acima, sabemos que 39% da população ativa é de mulheres. Sabemos, então, que os demais são homens. Sabemos também que a porcentagem de mulheres desempregadas é de 22% e de homens é de 14%.

Finalmente, também sabemos que a probabilidade de uma pessoa escolhida aleatoriamente estar desempregada é de 0,17. Então, se aplicarmos a fórmula do teorema de Bayes, o resultado que obteremos é de que existe uma probabilidade de 0,5 que uma pessoa escolhida aleatoriamente, dentre todas as que estão desempregadas, seja uma mulher.

P (M | P) = (P (M) * P (P | M) / P (P)) = (0,22 * 0,39) / 0,17 = 0,5

Nos despedimos deste artigo de probabilidade fazendo referência a uma das confusões mais frequentes em relação à probabilidade. Esta varia entre 1 e 0, nunca deixando essas margens, sendo 1 a probabilidade de um evento seguro e 0 a probabilidade de um evento impossível.